In this section, we look at some specific linear transformations from \(\R^2\) to \(R^2\) and how it transforms the unit square. Readers are encouraged to draw figures.
Fix a positive real number \(a\) and define \(D_a\colon \R^n\to \R^n\) by \(D_a(x)=ax\text{.}\) It is a linear map which is induced by the scalar matrix \(a I_{n}\text{.}\) ( \(D_a\) is called a dilation if \(a > 0\) and a contraction if \(a\lt 1\text{.}\)) Refer to Figure 3.4.18\(D_a\colon \R^2\to \R^2\) with \(a=2\) and \(a=1/2\text{.}\)
Figure3.4.18.Dilations with \(a=1/4\) and \(a=2\text{.}\)
Let \(a\) and \(b\) be two positive real numbers and \(A=\begin{bmatrix}a \amp 0
\\0 \amp b \end{bmatrix}\text{.}\) Define \(T\colon\R^2\to \R^2\) by \(T(x)=Ax\text{.}\) Then (i) \(T\) is stretching by a factor \(a\) along \(x\)-axis and by a factor \(b\) along \(y\)-axis if \(a,b >1\) and (ii) \(T\) is contraction by a factor \(a\) along \(x\)-axis followed by a factor \(b\) along \(y\)-axis if \(0\lt a,b\lt 1\text{.}\) Refer to Figure 3.4.20 for stretching along \(x\) by 2 and \(y\)-axes by 1.5.
Figure3.4.20.Stretching along \(x\) by 2 and \(y\)-axes by 1.5.
The follow iteract is generated using slate. You can change the input matrix and vectors and submit to see the image of vectors. Additionally, try to use the above tranformations defined such expansion, compression and shers and explore the same.
Let us explore, how a linear transformation tranforms a grayscale image. A grayscale image is simply a 2-dimensional array (matrix) where each entry represents the intensity of light at a particular pixel. We will explain two types of transformations, scaling the intesity and rotation by an angle to a given image.
We use the transformation \(T(P)=\alpha P\text{,}\) where \(\alpha\geq 1\) is the brightness of the image. Let us take \(\alpha =1.2\) about 20/% increase in the brightness. On each pixel \(p_{ij}\) of the image \(P\text{,}\) we have \(Q=TP\text{,}\) where \(q_{ij}=\min\{\alpha
p_{pij},255\}\text{.}\) Here min~255 ensures the brightness values stay within valid pixel range.
\begin{equation*}
\begin{pmatrix}
x' \\
y' \\
1
\end{pmatrix}
=
\begin{pmatrix}
a \amp b \amp c \\
d \amp e \amp f \\
0 \amp 0 \amp 1
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
\end{equation*}
Hence we get
\begin{equation*}
x' = a \cdot x + b \cdot y + c, \quad y' = d \cdot x + e \cdot y + f.
\end{equation*}
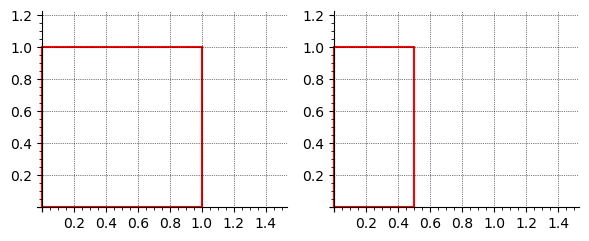
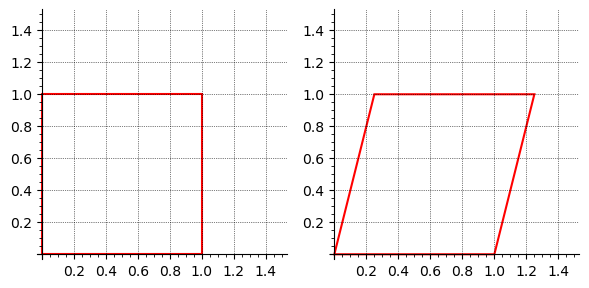
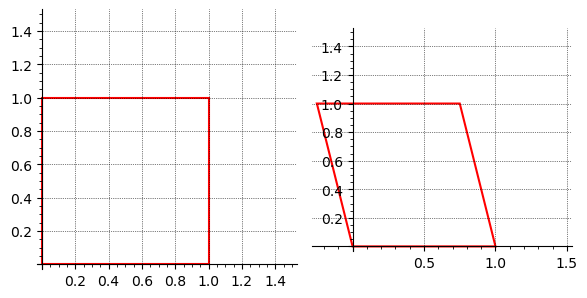
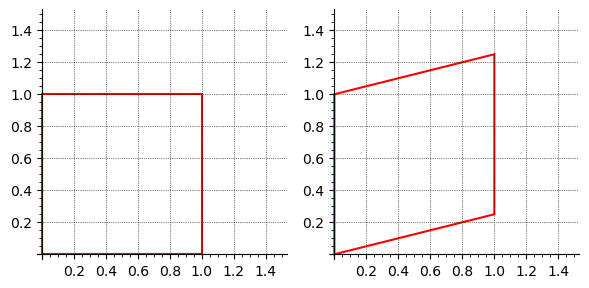
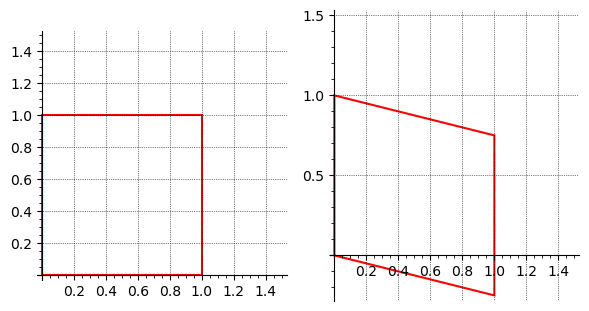
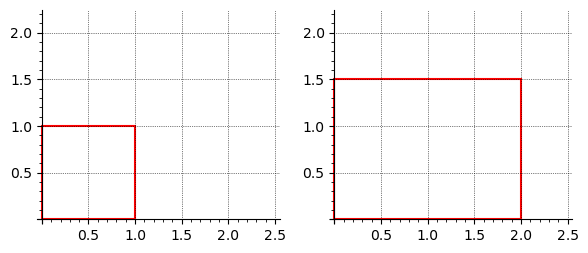
For a shear in the \(x\)-direction, we wish to shift \(x\) proportionally to \(y\) while leaving \(y\) unchanged. This corresponds to:
\begin{equation*}
a = 1, \quad b = k, \quad c = 0,
\quad d = 0, \quad e = 1, \quad f = 0
\end{equation*}
where \(k\) is the shear factor. Thus, the shear matrix becomes:
In Python’s Pillow library, the transform method uses parameters \((a, b, c, d, e, f)\) corresponding to the first two rows of the above matrix, that is,
A shear transformation in three dimensions is a type of linear transformation that shifts one coordinate axis in proportion to another, while keeping at least one direction fixed. Unlike scaling (which stretches or compresses) or rotation (which changes orientation), shear slants the shape without changing its volume (if the determinant of the shear matrix is 1).
For example, if \(s_{xy} = 1\text{,}\) then the \(x\)-coordinate increases in proportion to \(y\text{,}\) creating a slant of the cube in the \(x\)-direction depending on how far a point lies along the \(y\)-axis.
